二叉树遍历代码模板

1、二叉树的定义

strcut TreeNode{
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : val(x),left(NULL),right(NULL){};
}

2、二叉树的遍历

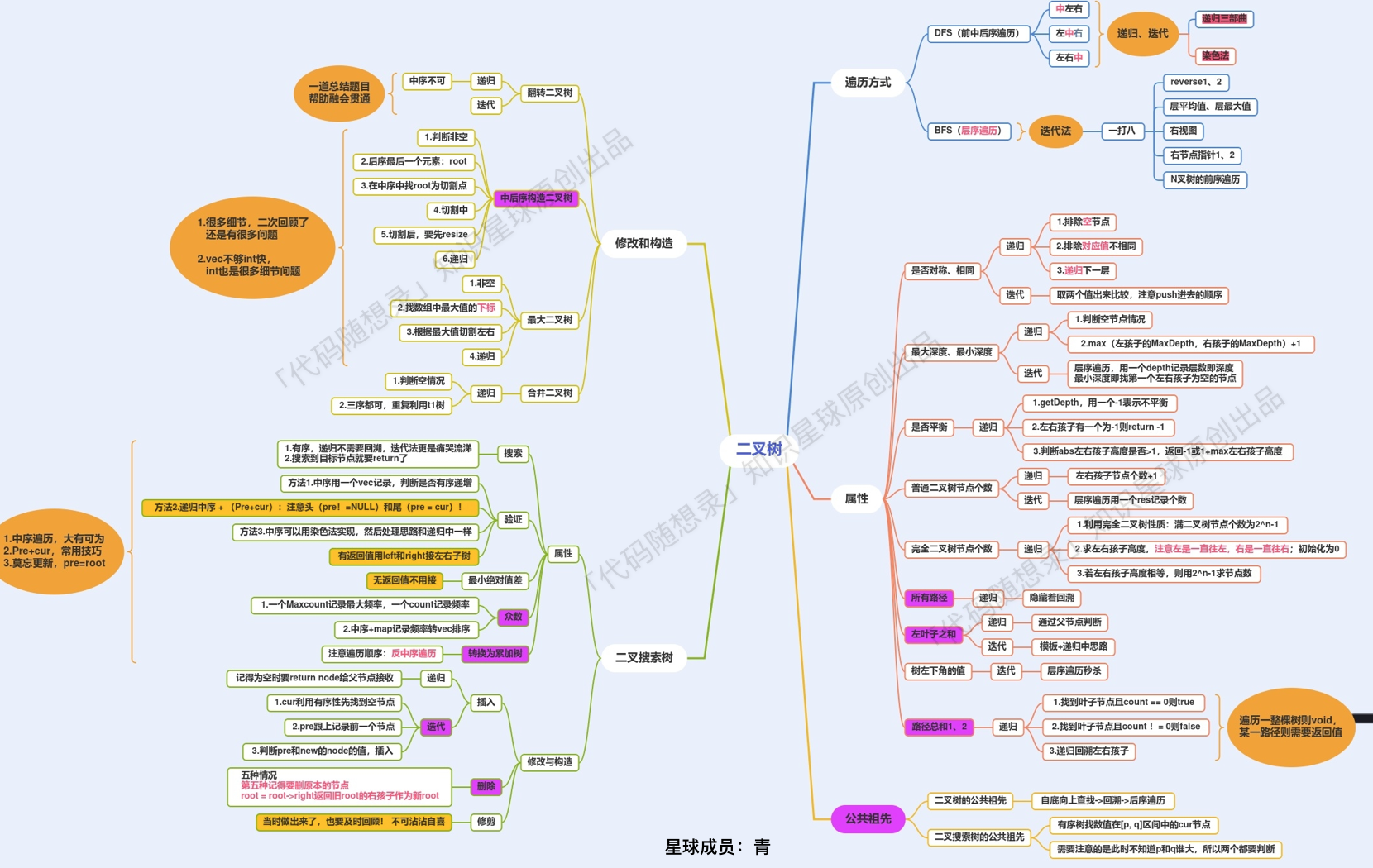
• 深度优先遍历
  • 前序遍历（递归法，迭代法）
  • 中序遍历（递归法，迭代法）
  • 后序遍历（递归法，迭代法）
• 广度优先遍历
  • 层次遍历（迭代法）

前/中/后序遍历：

class Solution{
public:
    // 前序遍历
    void traversal(TreeNode* cur,vector<int>& res){ // 要加&
        if(cur == NULL){
            return;        
        }    
        res.push_back(cur->val);   // 根
        traversal(cur->left,res);  // 左
        traversal(cur->right,res); // 右
    }
    
    // 中序遍历
    void traversal(TreeNode* cur, vector<int>& vec) {
        if (cur == NULL){
            return;
        }
        traversal(cur->left, vec);  // 左
        vec.push_back(cur->val);    // 根
        traversal(cur->right, vec); // 右
    }
    
    // 后序遍历
    void traversal(TreeNode* cur, vector<int>& vec) {
        if (cur == NULL){
            return;
        }
        traversal(cur->left, vec);  // 左
        traversal(cur->right, vec); // 右
        vec.push_back(cur->val);    // 根
    }
    
    vector<int> PreorderTraversal(TreeNode* root){
        vector<int> res;
        traversal(root,res);
        return res;
    }
}

层序遍历：

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> q;
        vector<vector<int>> res;
        if(root != nullptr){
            q.push(root);
        }
        while(!q.empty()){
            vector<int> temp;
            int size = q.size(); // 存放这一层节点个数
            for(int i = 0;i < size;i++){
                TreeNode* p = q.front();
                q.pop();
                temp.push_back(p->val);
                if(p->left != nullptr){
                    q.push(p->left);
                }
                if(p->right != nullptr){
                    q.push(p->right);
                }
            }
            res.push_back(temp);
        }
        return res;
    }
};
// 输入：root = [3,9,20,null,null,15,7]    输出：[[3],[9,20],[15,7]]

• 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数。
• 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数。

求深度可以从上到下去查，所以需要前序遍历（根左右），而高度需要从下到上去查，所以要后序遍历（左右根）

3、二叉搜索树（二叉排序树）

遇到在二叉搜索树（二叉排序树）上求什么最值，求差值之类的，都要思考一下二叉搜索树可是有序的，要利用好这一特点

如果递归函数有返回值，如何区分要搜索一条边，还是搜索整个树：

搜索一条边的写法：

if (递归函数(root->left)) return ;
if (递归函数(root->right)) return ;

搜索整个树写法：

left = 递归函数(root->left);
right = 递归函数(root->right);
left与right的逻辑处理;

选择什么遍历顺序:

• 涉及到二叉树的构造，无论普通二叉树还是二叉搜索树一定前序，都是先构造中节点。
• 求普通二叉树的属性，一般是后序，一般要通过递归函数的返回值做计算。(具体问题具体分析)也有用前序的
• 求二叉搜索树的属性，一定是中序了，要不白瞎了有序性了。